• Classical Approach (古典概型/等可能概型）
• Bayes’ Theorem (贝叶斯定理)

Classical Approach (古典概型/等可能概型）

Requirements:

1. Finite sample space (试验的样本空间只包含有限个元素)

2. Each event shares the same odd of occurrence (试验中的每个基本事件发生的可能性相同)

Formula: \(p = h/n\)
where h is the number of ways an event can occur and n is the total number of possible ways in the sample space.

Examples：

• Example 1: Tossing a coin n times. 抛一枚硬币n次. 可能存在的Head 和 Tail 的搭配总数是有限的，并且每次抛硬币head 或者tail的可能性都是1/2
• Example 2: The probably of N people in a party having the same birthday. N个人在一年365天中同一天过生日的概率问题也是古典概型。因为每个人的生日在1年365天任意一天的概率均为1/365，这些人过生日的可能配搭种类也是有限的。

Bayes’ Theorem (贝叶斯定理)

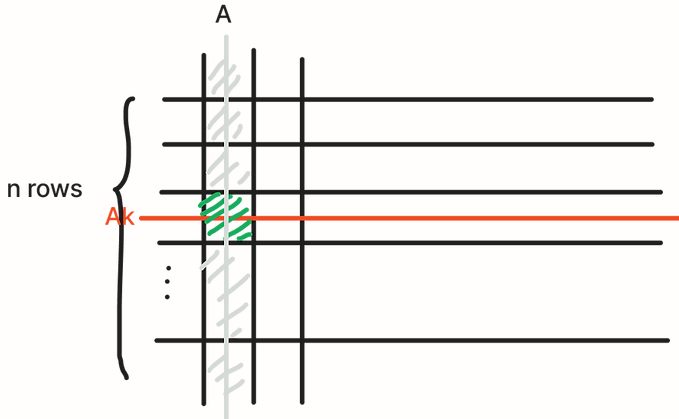
A visual demonstration of Bayes’ theorem is as follows. The theorem can be interpreted as calculating the percentage of the green area in the sum of the gray area:

1. $$ P(Ak)P(A

   Ak) $$ finds the green area

2. The sum of $$ P(Aj)P(A

   Aj) (j=1,…,n) $$ is the grey area

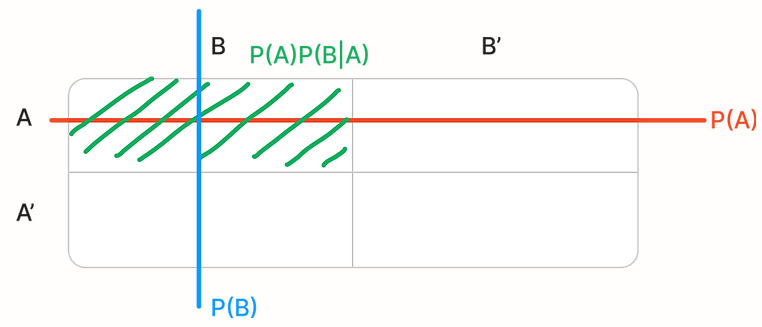
Given two mutually executive events A and B, the Bayes’ rule can be denoted as follows: \(P(A|B) = (P(A)P(B|A))/P(B)\)

To visualize the equation, you can think of a 2x2 table where the rows representing A and A’ respectively and the columns representing B and B’. As shown in the following figure:

1. P(A) is the probability of the event A in the sample space. Denoted as the entire row of A in the figure.
2. P(B) is the probability of the event B in the sample space. Denote as the column of B in the figure.

3. P(A)P(B

   A) is the probability of event B given event A occurs in the sample space and is denoted in the green area in the figure. Note that this area does not represent the probability of event B given event A. To calculate it, you need to cancel out the sample space by dividing P(B).