A feedforward neural network
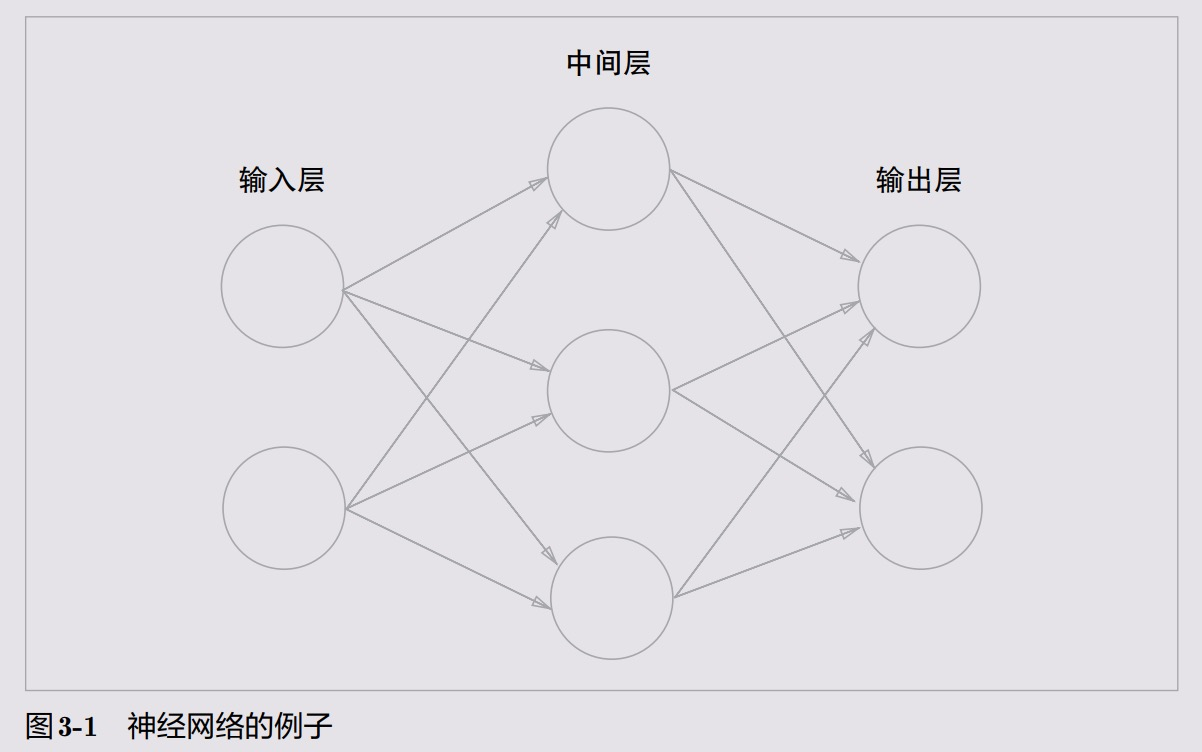
If we use a diagram to represent a neural network, as shown in Figure 3-1.
We call the far left column the input layer, the far right column the output layer, and the middle column the middle layer.
The middle layer is sometimes also called the hidden layer. The term “hidden” means that the neurons in the hidden layer (unlike those in the input and output layers) are not visible to the naked eye.
In Figure 3-1, the 0th layer corresponds to the input layer, the 1st layer corresponds to the middle layer, and the 2nd layer corresponds to the output layer.
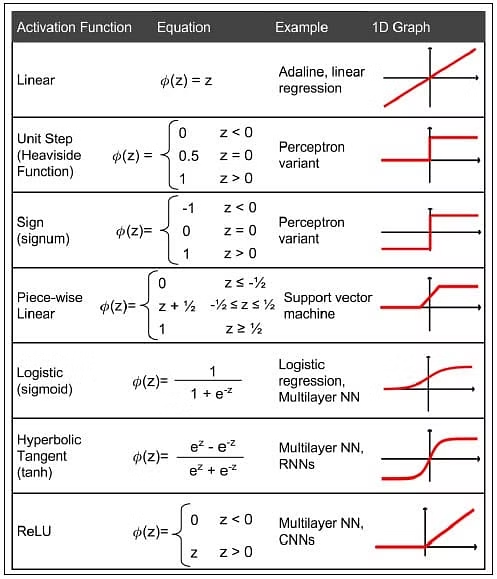
Activation functions
In a neural network, the activation function \(h(x)\) receives the weighted sum of the inputs and biases \(a = w_1x_1 + w_2x_2 + \ldots + w_nx_n + b\) and decides whether the neuron should be activated or not.
The activation function introduces non-linearity to the neural network, allowing it to learn complex patterns in the data. The following diagram shows the computation of an activation function:
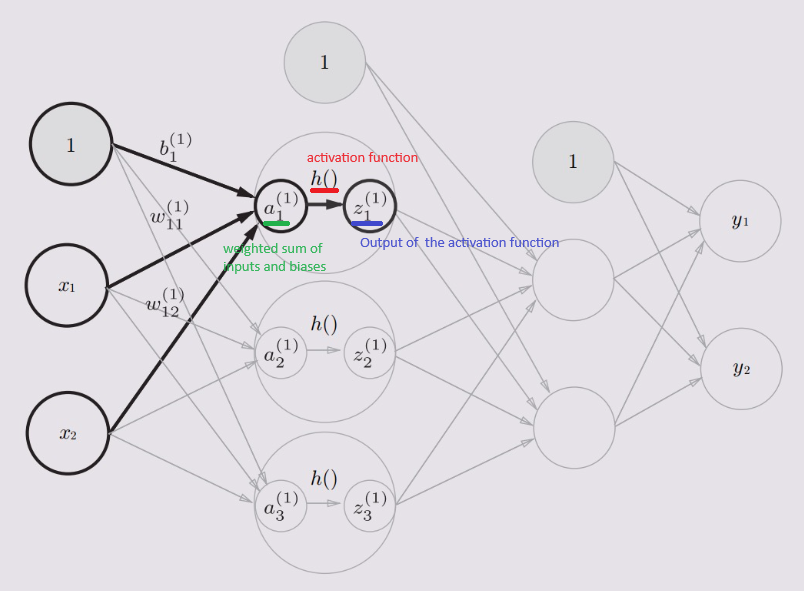The weighted sum of the inputs and the bias is denoted in node a, then it is passed through the activation function \(h(x)\) to produce the output \(z\).
Types of activation functions
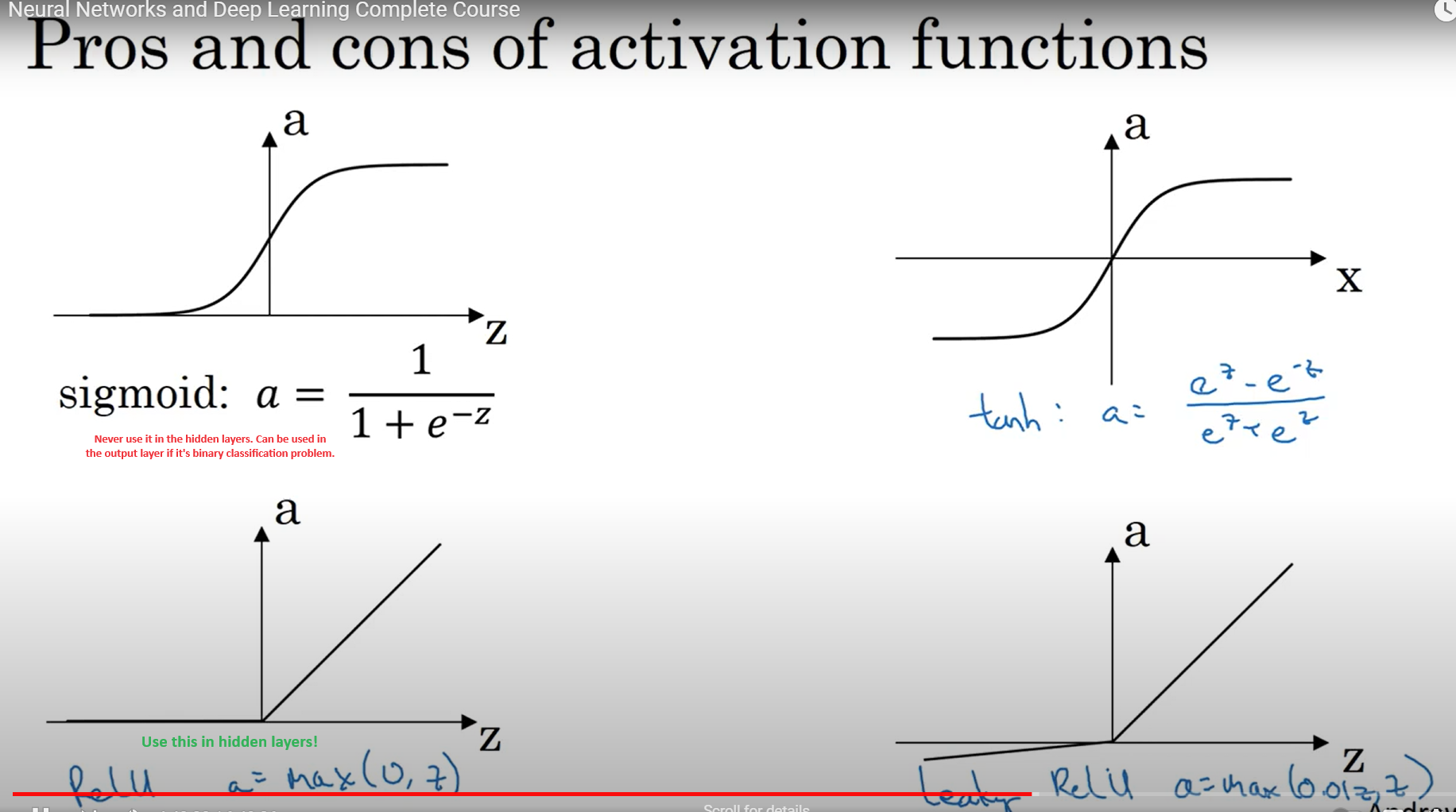
Sigmoid function
The sigmoid function is a type of activation function that is used to introduce non-linearity in the neural network. It squashes the input values between 0 and 1. The formula for the sigmoid function is given by: \(\sigma(z) = \frac{1}{1 + e^{-z}}\)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x=np.array([-1.0,1.0,2.0])
sigmoid(x)
#array([0.26894142, 0.73105858, 0.88079708])
Step function
The step function is a type of activation function that produces a binary output. If the input is greater than a certain threshold, the neuron is activated and produces an output of 1; otherwise, it produces an output of 0. The formula for the step function is given by: \(f(z) = \begin{cases} 1 & \text{if } z \geq 0 \\ 0 & \text{if } z < 0 \end{cases}\)
def step_function(x):
return np.array(x > 0, dtype=np.int)
x=np.array([-1.0,1.0,2.0])
step_function(x)
#array([0, 1, 1])
ReLU function
The ReLU function (Rectified Linear Unit) is a type of activation function that introduces non-linearity in the neural network. It returns 0 if the input is less than 0, and returns the input itself if it is greater than 0. The formula for the ReLU function is given by: \(f(z) = \begin{cases} z & \text{if } z \geq 0 \\ 0 & \text{if } z < 0 \end{cases}\)
def relu(x):
return np.maximum(0, x)
x=np.array([-1.0,1.0,2.0])
relu(x)
#array([0., 1., 2.])
Softmax function
The softmax function is a type of activation function that is used in the output layer of a neural network to produce a probability distribution over multiple classes. It squashes the input values between 0 and 1 and normalizes them to sum up to 1. The formula for the softmax function is given by: \(\text{softmax}(z)_i = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}}\)
def softmax(x):
return np.exp(x) / np.sum(np.exp(x), axis=0)
x=np.array([1.0,2.0,3.0])
softmax(x)
#array([0.09003057, 0.24472847, 0.66524096])
Caution: The softmax function is sensitive to large input values, which can lead to numerical instability.
To avoid this, it is common to subtract the maximum value from the input values before applying the softmax function. The modified softmax function is given by: \(\text{softmax}(z)_i = \frac{e^{z_i - \max(z)}}{\sum_{j=1}^{n} e^{z_j - \max(z)}}\)
def softmax(x):
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum(axis=0)
x=np.array([1.0,2.0,3.0])
softmax(x)
#array([0.09003057, 0.24472847, 0.66524096])
Common activation functions
